The Golden Number

When someone says "Maths", maybe the most iconic number they can come up is pi, or rather the e number. But what if there's another number, mucho more important than this other two? Well, it actually exists, and it's called the phi number, also known as the golden ratio.

The value of this number is 1.6180339887 and it represents a proportion between two segments:

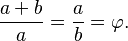
The usage of this numbers has been developed by years. Euclid was the first Mathematician who studied the divinal proportion in a regular pentagon and a golden rectangle. By cutting the gold rectangle, it creates a square and a smaller rectangle with the same aspect radio. The most remarkable ones in Mathemathics are Michael Maestlin, who published in 1597 a decimal approximation of the golden ratio, Fibonacci mentioned the numerical series, Johannnes Kepler created the Kepler triangles, a combination of phi along with the Theorem of Pythagoras, and Édouard Lucas gave us the Fibonacci sequence, a numerical sequence.

There are several applications for this peculiar number. Some of them are related to Architecture, painting, design(bookdesign, postcards, playing cards, posters, wide-screen televisions...), music, narute and optimization.

Let's go deeper into the number. This is the negative root of the number, known as the conjugate root

Taking it's absolute value and dividing one by it, we have a new number called golden ratio conjugate.

The golden ratio and the golden ratio conjugate can be expressed like this

Those two expression are used as a scale for every proportion. For example:

The major usages of the number is seen in triangles and pyramids, containing different symmetries.